Rubiks Cubes! I cant solve them to completetion for the life of me. But now I can just solve them using an AI.
But before jumping into heuristics, A* algorithms, and all kinds of solving. First, let us consider a random Rubiks Cube itself. Is the cube actually solveable in the first place? Can we go from the random state pictured above to a solved cube?
The answer is no. The Rubiks Cube parity has been altered!
Intro
Note that this is for a classic Rubiks cube (3x3x3).
Quite simply, the cube’s corners have been twisted. Its the equivalent of taking the stickers off a normal Rubiks Cube and sticking them into different positions. It makes the cube impossible to solve. Or at least, the chances of getting random stickers into a solveable position is tough. The total number of possible valid Rubiks Cube scrambles is 43 quintillion (8! x 3^7 x (12!/2) x 2^11). The total number of possible Rubiks Cube scrambles in total (both valid and invalid) is a rediculous 519 quintillion . (8! x 3^8 x 12! x 2^12) And that’s not including the possibility of switching stickers (invalid cubie possibilities, but more on that later). So the number is even more astronomical.
You have a 1/12 chance for a random Rubiks Cube to be valid (that was made with valid cube colors)
What is a Rubiks Cube made of?
As a 2D representation, a Rubiks Cube has unique 54 squares (or stickers) and there are 6 colors represented on each of the 6 faces of the cube. So there are 9 squares of each color. Usually Red, Orange, Yellow, Green, Blue, White.
There is more to a Rubiks Cube though. Categorically, you can split a Rubiks Cube up into 3 types of “cubes”. Otherwise known as Cubies. Its easier to picture this in 3D. A Cubie is a 3D cube that represents part of the whole Cube.
There are 26 Cubies on a Rubiks Cube.
8 of them are Corner Cubies and 12 of them are Edge Cubies. The other 6 are Center Cubies.
The main difference between corner and edge cubies are that corner cubies have 3 different colors and edge cubies have 2 different colors. Center cubies only have 1 and its impossible to actually move a center cubie.
So right off the bat, there are a bunch of ways to tell if a Cubie is not solveable. It has to have 6 colors and 9 stickers or squares of each color. Each color has to be represented in a center cubie only once. No more, no less. If you peel off a center sticker and replace it with a different color, the cube is immediately not “solveable”.
However, just these alone are not enough. You need more than that. Namely, none of those checks look at parity. The parity of a cube needs to be correct in order for all the cubies to be able to properly be orientated in their home positions. Home positions in a Rubiks Cube is the position on a face in which the cubie is facing the right direction. For example, the Blue/Yellow edge cubie has its Blue side touching the Blue center and the Yellow side is touching the Yellow Center. Its in its home position. When all cubies are in their home position with correct orientation, the cubie is solved.
So in my original example at the top of the page, the picture has the corners all twisted. The parity is off because we’ve twisted corner cubies and their orientations can never be correct with the rest of the cube now. Those corners can never be in the right position and orientation without the rest of the cube being incorrect!
So how does one check for these? Three tests:
- Permutation
- Corner Parity
- Edge Parity
Believe it or not, I found an incredible lack of information online regarding these tests. The best rescources I can find through Google were here, here and here, and only the latter skantly goes into detail how to actually perform the tests. And any information about performing the tests is either a little off or under explained! At least, for example, permutation tests only consider one side of a cube and not the WHOLE cube. So thats why I felt it necessary to make this lengthy blog in detail.
Permutation Test
In my opinion, the easiest test to implement.
Simply consider each unqiue Edge and Corner Cubie as an arbitrary unique number. Seperately for Edge and Corner, pick a fixed cubie to start from and consider what # is actually in that position and repeat for all Edges or Corners. Then if the total number of inversions to make both lists (edges and corners) ordered is even, you have a valid permutation.
Rewind.
Lets start with edges, we have 12 unqiue cubies for them.
RW – RG – RB – RY – GW – GY – GO – YB – YO – BW – BO – OW
0 – 1 – 2 – 3 – 4 – 5 – 6 – 7 – 8 – 9 – 10 – 11
This is the order I went with. I number each of these cubies 0 to 11. Basically, if I look at any edge on the cubie in my program (or physically in real life), you can tell that if the edge cubie is R & Y or Y & R, then its value is 3. R & W or W & R is 0. And so on.
To make things easier, its also nice to look at the positions in the same way. So if I say “go to position 0 for edges”, you’d look at where RW is supposed to be (its home position). Sometimes this is hard for newbies to Rubiks Cubes when someone says go look at a position. Its where the Red and White cubie would be if you would look at a solved cube. That never changes! What’s in that position changes.
So consider the list G = { 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12}
We’d agree with the explanation above that is “solved”. It doesn’t mean the cube itself is actually solved, but that order is how we expect the cubes to be in when we solve a cube.
If we have the list A = {7, 6, 4, 0, 11, 10, 5, 1, 9, 8, 2, 3}
That means YB is where RW should be, GO is where RG should be, and so on.
From this list, find the number of inversions to get from A to G. Inversions are simply the number of times each number has to be swapped to get into sorted order. Read it from left to right to understance easier.
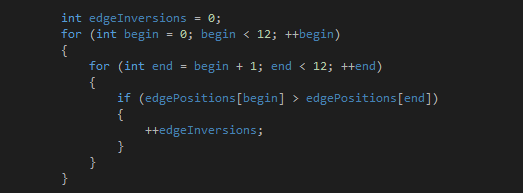
Very simple inversion code:
Perhaps A is a bit of a complex example, but it would take 38 inversions to get to list G from it.
Take the results from doing this with corners, handled the exact same way (but from 0 to 7 instead), and add the results together.
If the result of cornerInversions + edgeInversions is even then a whopping 1/2 of invalid possibilities are rejected! Its an easy and effective test to do!
If its odd, then two cubies or more are out of parity. They’ve been swapped, possibly from deconstructing and reconstructing the cube. (eg, you switched BO and OW or something)
The reason for this test is because each inversion is a “swap”, and there can never be a total number of odd swaps. In other words, no matter how many times you turn a Rubiks cube, if they’re legal (valid) twists of the cube – they always result in even swaps in total.
Corner Parity Test
A bit tougher. Look at a face of your cube straight on. Never change the orientation of the cube from here on out. Always look at that face and always make sure the top and bottom colors never change.
For example. if I look at the Orange face on a classic Rubiks Cube and Yellow is the top face, then White is garunteed to be my bottom face. Blue is my right face. Green is my left face. And Red is my back face. Choose however you want to look at it, but just make sure you never change it in the middle of Corner and Edge Parity tests.
We’re going to do something similar to the permutations in regards to positions. So from 0 to 7, we’re going to look at these positions the same all the time. Its contents can be different, but the positions are where we expect the cubes in their home positions.
For example,
RGW – RBW – RGY – RBY – GOW – GOY – YOB – BOW
0 – 1 – 2 – 3 – 4 – 5 – 6 – 7
When I look at position 2, it could have any corner cubie in any orientation in it, but its where RGY should be if its a solved cube.
Starting from 0, look at every position to 7 and consider the orientation of the cubie. What do I mean by that? Again, in my example picture, the corner cubies have been twisted. We’re testing for this!
How its going to work is we treat the top and bottom colors as the same. In other words, forget the sides of the corner cubies that are Yellow and White in my example. Treat Yellow and White as if they were exactly the same color. Its kind of weird, but bear with me.
If the White or Yellow part of a corner cubie is touching White or Yellow center, then we know that our cubie is correctly orientated. If the top/bottom color is not touching the center of their friend, then we know that the cubie is not correctly orientated. The issue is the cubie can be two kinds of not correct – clockwise or counter clockwise.
The way to tell which kind of incorrect orientation is by imaginging you’re twisting the corner cubie yourself. You’re pulling out that corner cubie from your Rubiks Cube and physically rotating it in your mind. How many clockwise turns does it take to get that top/bottom color to touch ? One or two turns?
An important thing to remember is that using your left or right hand matters here. A clockwise turn with your left hand is not the “same” turn with your right hand.
Its tough to explain in words – here might be a few pictures to help:
This is where corner positions play an important role. For each of the corner cubie positions we discussed before from 0 to 7, you have to play with your corners to figure out which corners orientations take 2 rotations and which corners only take 1. You can determine this and kind of hard code it into your program by considering which side White or Yellow is on (or whatever your top color is) and simply loop through your structure of 3 colors (corner cubie). If the White or Yellow cubie is in corner X (0-7) and the position inside your corner cubie is Y (0-2), then its either correctly, clockwise, or counterclockwise orientated.
Those three results should be numbered. 0 for correct, 1 for clockwise, 2 for counterclockwise.
For each of your 8 corner cubies, add those numbers together. If the total number is divisible by 3, then your corner cubies have a valid parity. Thats 1/3 invalid possibilities rejected for your Cube!
Edge Parity Test
The hardest test to program out. I personally went through and found every possibility for this on my Rubiks Cube and hard coded this test pretty throughoughly at first. But, there is an easier way to figure this out on the fly. It has to do with opposing faces, much similar to the Top/Bottom (White/Yellow) in the Corner Parity Test.
Again, make sure you look at the same face as you did before with the same orientation in the Corner Parity Test too. (Mine was looking at orange, Yellow on Top, White on the bottom)
White and Yellow are opposing faces for me. Blue and Green are also opposing. And so is Red and Orange. Think of the opposing colors as the same colors, again similar to White/Yellow. If the opposing color is correctly touching the center opposing color correctly, then it is correctly orientated.
For example, Orange and Red are again opposing colors. If you have Red/White edge in the position where Orange/Yellow should be, and Red is touching Orange center and White is touching Yellow, your cube is not correctly orientated!
For every edge cubie, go through each position (0 to 11) and perform this test. If its not correctly orientated, increment a counter. If that counter is divisible by 2 after testing every edge cubie, then you’ve just rejected another 1/2 of invalid configurations!

Blue-Red is correctly orientated! Notice how only the right and top faces needed to be rotated. NOT the front or back.
But first, why does this work? If you read Arjun’s page earlier, it has to do with using the front and back faces to flip edges. If you’re looking at a cube at the orange face, then in order to get an incorrectly orientated edge into position, you need to use either the back or front faces to turn. For correctly orientated edges, you don’t need to do this! You can use the Top, Bottom, Left, or Right faces to get that cubie into home position with the right orientation.
Here’s a good video about edges as well:
Results
And that’s it. If you cube goes through all 3 of these, and return true, you have a valid Rubiks Cube that can be solved! If even one fails, you have an invalid cube that cannot be solved.
This branch on Github has only the code pertaining to Rubiks Cube parity tests done in C++. I hard coded EdgeParity, but you can do it using the method with opposing colors too.
This is just part one of several. I’ll cover how I designed and implemented my Rubiks Cube representation next time.